Poker Combinations: 10 Types Of Hands That Can Be Created
In poker, the word combo refers to a single occurrence of a certain holding. In Hold 'em, for example, there are six distinct ways to be dealt pocket Aces preflop, thus there are six potential pocket Ace combinations. Each off-suit hand has 12 distinct combinations, while each suited hand has four different possibilities.
Author:James PierceReviewer:Paolo ReynaSep 13, 20212K Shares137.3K Views

In poker, the word combo refers to a single occurrence of a certain holding. In Hold 'em, for example, there are six distinct ways to be dealt pocket Aces preflop, thus there are six potential pocket Ace combinations. Each off-suit hand has 12 distinct combinations, while each suited hand has four different possibilities. Combinations are often shortened to combos in most talks. Although it may theoretically be used to describe a particular combination of cards in any variation, the word "combinations" (combos for short) is usually used when discussing either Hold'em or Omaha variants.
In Hold 'em, there are 1326 different combinations of two cards that may be dealt with before the flip. Aside from the suits, these cards are essentially similar. I.e., despite their strength is the same, both 7/8 and 7/8 are distinct combinations of hole-cards. If we disregard the suits, there are a total of 169 different preflop holdings in Hold'em.
Each matched hand has four different combinations, such as 788. Each unsuited hand has 12 possible combinations (not counting pocket pairs), such as AQ. Each pocket pair has six different combinations, such as 666.
After the community cards are dealt with, the potential combinations of each beginning hand alter. On a KT6 flop, for example, there are no longer six possible TT combinations as a player's hole cards. (In the strategy application section, there's more on counting combinations.)
The number of potential starting hand combinations grows rapidly in a four-card poker variation like Pot Limit Omaha. In PLO, there are 270,725 potential four-card starting hand combinations.
Using Poker Combinations As Part Of Poker Strategy
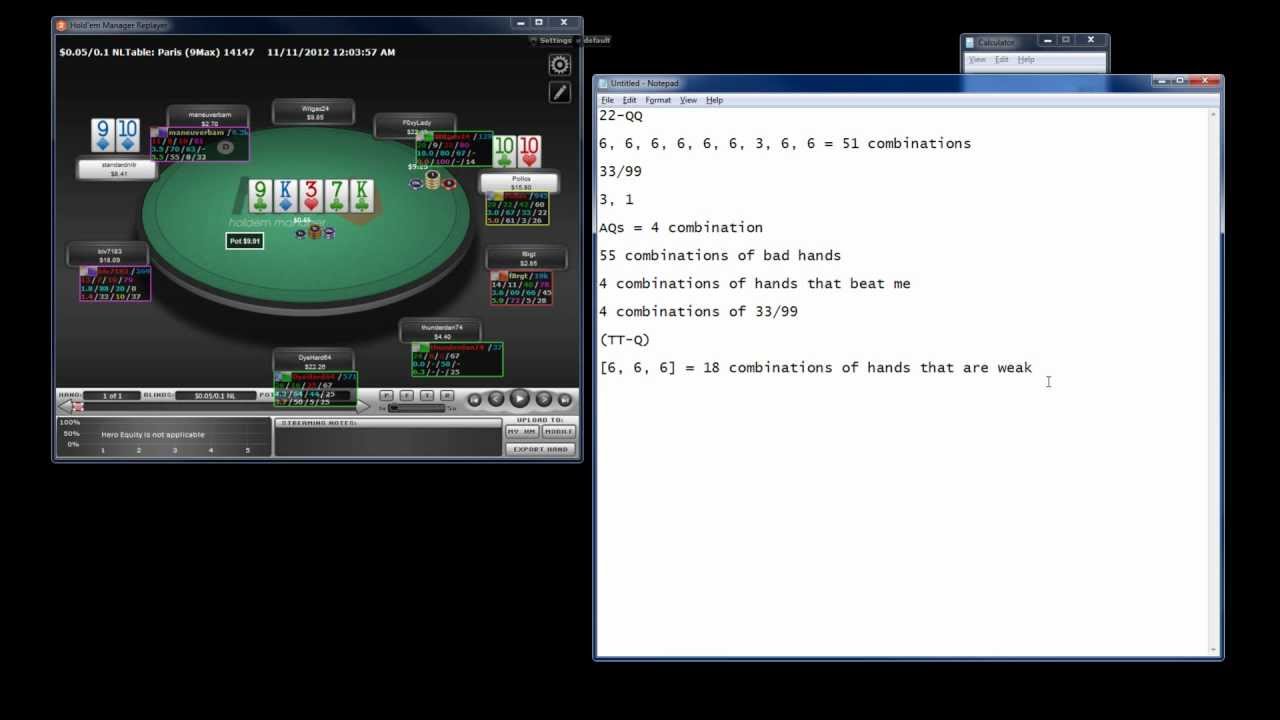
In this article, we'll go over how to count combinations in a post-flop Hold'em situation. We may get insight into the optimal play by counting the exact number of various kinds of holds inside our opponent's range. Combinatorics is typically used when we are in a tight position. Counting our opponents' combinations would be superfluous if our choice was simple. Consider the following situation:
In a scenario when we only have a bluff catcher, our opponent bets half the pot on the river. He has 15 valid value combinations, according to our calculations. To address this question, we must first figure out our pot-odds. We would be spending 25% of the entire pot if we made the call, which means we would have to win more than 25% of the time to earn a profit. (This is also known as the 3:1 pot odds.) In order for our call to break even, we need our opponent to be bluffing at least 25% of the time. As a result, if our opponent had 5 bluff combinations, our call would be even. Our call would start to earn money if he had more bluff combinations.
We could undertake the combinatorics work if we thought it was a close call. However, if we have a read that our opponent never bluffs in a certain location, we may fold without any combination counting.
Counting Postflop Hold 'em Combinations. Holdings without a partner. We multiply the number of first cards left in the deck by the number of second cards left in the deck to get the remaining possibilities of an unpaired (preflop) hand. Let's look at an example to illustrate this.
- There is no King or Jack on the board, which means the deck is down to four Kings and four Jacks. 4 4 = 16 KJ combinations
- Because there is already a King out there, there are only three Kings remaining in the deck. 4 * 3 = 12 KJ combinations
- The deck is down to two Jacks and three Kings. KJ may be combined in 3 * 2 = 6 different ways.
Paired Holdings is a company that invests in other companies.
In this case, we're talking about pocket pairs when we say "paired" holdings. The criteria for calculating how many matched combinations are left in the deck vary somewhat. We increase the number of cards left of that particular rank by "itself minus one" and then divide it by two. Let's see how it works like a formula.
- There are no sixes on the board texture, indicating that there are only four cards remaining in the deck.2) There is already one six in play, therefore there are only three cards remaining in the deck. (3 * (3-1))/2 = 6 different 66 combinations.
- There are only two sixes remaining in the deck since there are already two sixes out there. (2 * (2-1))/2 = 66 possible combinations
As a result, combinations may be utilized to determine the weighting of different kinds of hands. Players may be surprised to discover that on boards with a potential straight, there are more straight combinations than flushes. There are 16 potential straight combinations on a QAT texture, but only 9 possible set combinations.

Permutations and Combinations - 5 Card Poker Hands
Hand Combos In Poker
The number of distinct card combinations that may make up a beginning hand is referred to as a combo. A deck of cards has 52 cards, 13 of each suit and four of each rank. This implies that there are:
- Every unpaired hand has 16 potential hand combinations.
- Each unpaired offsuit hand has 12 different hand combinations.
- Each suited hand has four hand combinations.
- Each pocket pair has six potential combinations.
- From Aces to 3-2 offsuit, there are 1326 possible permutations of all the hands that may be dealt before the flip.

Poker Combos: Everything You Need To Know | SplitSuit
There Are 10 Different Types Of Hands That May Be Created
- Royal Flush-all five cards in the sequence are of the same suit. J – Q – K – A – 10 – J – Q – K – A – 10 – J – Q – K – A – 10 – J – Q – K – A – 10 – J –
- Straight Flush-all five cards in a straight flush are of the same suit and rank. (It's worth noting that a royal flush is only the highest-ranking straight flush.)
- Four-of-a-Kind (abbreviated as 4OAK in this article) — a hand with four of a kind. When all four cards have the same rank,
- Full House — a hand with one pair of cards and a three-of-a-kind of a different suit. in comparison to the couple
- Flush-all five cards are of the same suit, but they are not all ranked in the same order. Straight-all five cards have the same rank, but they aren't all of the same suit.
- Three-of-a-Kind (abbreviated as 3OAK) — a hand with three of a kind. All of the cards are of the same rank, while the other two are of different rankings.
- 3OAK as well as each other.
- Two Pair-two pairs of two identical cards (the rankings of each pair are the same). To prevent a 4OAK, the ranks must be different.)
- One Pair-of the five cards, only two are of the same rank as the other three. All of the cards have distinct rankings from one another and from the pair.
- High Card-a a hand in which no better hand could be created (i.e., a hand in which each of the cards is a high card). Each has a different rank than any other card, and the five cards are not all of the same suit or color.

Poker Hand Rankings | Poker Tutorials
Combinatorics Of Top Pairs
Making a particular hand is less probable when one of the cards required to create that hand is on the board. As a result, many ranges find it difficult to achieve a top pair.
Rafi has 15 top pair combinations on this board, but 36 no-pair combinations. This implies that he has already struck a top pair on 29 percent of his unpaired hands. By limiting your opponent's range, this technique may help you make smarter choices.
Combinatorics Of Flush Draws
Of the 93 hands that make it to the flip, Rafi's range will contain a diamond flush draw with 9 combinations. Because the T is a diamond, this range will provide a flush draw less often than it would otherwise. If the two bottom cards were diamonds, there would be an additional 5 flush draw possibilities (AT-T9), increasing the total to 14. That's around 15% of the hands raised, a 50% increase! Rafi's flush possibilities are severely limited by certain diamond turn cards.
If the flip card was the J, this range would include 5 flush combinations in a total of 89 hands or approximately 6% of flushes. This is because the J appeared in four of Rafi's flush draws from the flip. Rafi's chances of getting a flush would climb to 10% (9 of 90 hands) if the turn was the 4, almost doubling his chances from the J! Keep an eye out for flashcards with large range effects, like the J, and attempt to take advantage of the scenario when they land on the felt.

Combination formula | Probability and combinatorics | Probability and Statistics | Khan Academy
Combinatorics Of Sets
Set Combinatorics is a branch of mathematics concerned with the study of sets. The rarity with which sets arise is one of the reasons they are so precious. Rafi's range has formed a set with two of his pre-flop cards since the 3 and 2 are on the board (33 and 22). The number of possible combinations for 33 and 22 is reduced by half when one of each card is on the flop (from 6 combinations to 3).
When you have a top pair versus someone who is representing a set, knowing how difficult it is to have a set in a scenario is very helpful. Assume Rafi raises the flip against our c-bet with the aforementioned range. If the only hands he would raise for value are 33 and 22, but he would also mix in some bluffs with 44, his range is split 50/50 between value and bluffs.
How To Do Combinatorics In Poker

James Pierce
Author

Paolo Reyna
Reviewer
Latest Articles
Popular Articles
