Spontaneous Symmetry Breaking Explained
Taking a step back from the specifics of the different symmetries, it makes some general statements about how important and important symmetries are in physics. In that specific scenario, let us try to explain the Spontaneous Symmetry Breaking phenomenon.
Author:Paula M. GrahamReviewer:Rhyley CarneyJan 08, 202363.2K Shares1.3M Views
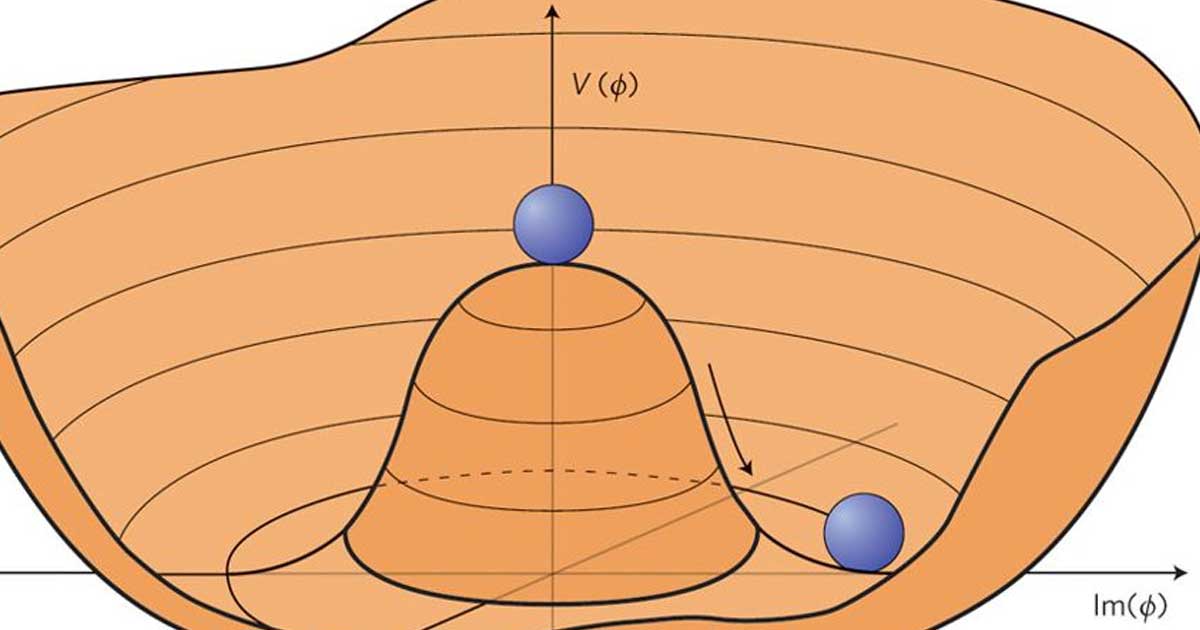
Modern basic physics is dominated by symmetry issues, both in quantum theory and relativity. The relevance of gauge symmetry, quantum particle identity in light of permutation symmetry, how to make sense of parity violations, the function of symmetry breaking, the empirical status of symmetry principles, and so on are all topics that philosophers are starting to pay more attention to.
These concerns are intimately related to classic philosophical difficulties in science, such as the validity of natural laws, the link between mathematics, physical theory, and reality, and the extent to which mathematics proposes novel physics.
This section begins with a brief overview of the historical origins and evolution of the symmetry notion used in modern research. It then moves on to discuss how this notion is applied in physics, distinguishing between two types of symmetry: symmetry principles and symmetry arguments.
It describes the many types of physical symmetry and the methods through which they were introduced into physics. Then, taking a step back from the specifics of the different symmetries, it makes some general statements about how important and important symmetries are in physics. In that specific scenario, let us try to explain the Spontaneous Symmetry Breakingphenomenon.
Symmetry Breaking
In physics, symmetry concepts are extremely significant. The right and left sides of an animal's anatomy, the round disc of the Sun and Moon, a wallpaper design, or even a repetitive musical beat, are all examples of space-time symmetry. And symmetry has evolved into a basic technique for describing physical rules. Symmetrical items have fewer aspects to describe and hold less information.
We must specify the topic as well as the number of times it is repeated, such as one home within a series of identical dwellings. These are some examples of scientific laws: At all times and in all locations, something remains the same. On the other hand, if a system passes through a phase transition to a more differentiated state, it will have more characteristics to describe and more information to store.
Water, for example, appears the same in all directions, yet it gets more intricate as it transforms and becomes a snowflake. Only six ways make a snowflake crystal appear the same. This is an example of broken symmetry. In the field of particle physics, symmetry breaking is just as crucial. It is the fundamental notion from which the theory of supersymmetry arose. Physicists think that immediately after the big bang, all-natural forces and elementary particles were identical. But symmetry was shattered in an instant.
The color interaction between quarks separated from the electroweak force first, and hadrons gained masses that were substantially different from leptons. After that, the electroweak force split into two parts. What is the relationship between electromagnetism and the weak force? and the list goes on. I believe you get the point. I don't want to add to your confusion with anymore broken symmetries.
Nambu Spontaneous Symmetry Breaking
The 2008 Nobel Prize in Physics was given to Yoichiro Nambu for "discovering spontaneous symmetry breakdown in subatomic physics."
The Nambu-Jona Lasinio Model is a non-linear nucleon model in which chiral symmetry is disrupted by chance. It depicts pions as a Nambu-Goldstone collective mode and dynamically creates mass for them (bound state).
It explained the pion's tiny mass in comparison to nucleons, provided a new derivation of the Goldberger-Treiman relations, and obtained universal findings in terms of the pion decay constant for low-energy pions and nucleons. A lot of things were in it, but it didn't have everything that led to the Standard Model of Elementary Particles or modern algebra.
Spontaneous Symmetry Breaking Use
There must be a system with numerous equally likely possibilities for spontaneous symmetry breakdown to occur. As a result, the system as a whole is symmetric in terms of these outcomes. A specified outcome must occur if the system is sampled (that is if the system is really used or interacted with in some manner).
Despite the fact that the system as a whole is symmetric, it is only ever experienced in one asymmetric state. As a result, in that theory, the symmetry is said to be spontaneously shattered. That each option is equally likely, on the other hand, is a reflection of the hidden symmetry, which is called "hidden symmetry." This has important formal implications.
When a theory is symmetric with regard to a symmetry group yet needs one of the group's elements to be distinct, this is known as "spontaneous symmetry breaking." It is not necessary for the theory to specify which member is distinct, merely that one is. From this point forward, the theory can be handled as if this element were separate, with the caveat that any findings obtained in this manner must be symmetrized by taking the average of each of the group's unique components.
The order parameter is a fundamental topic in physics theories. The system is in the ordered phase, and the symmetry is spontaneously broken if a field (typically a background field) obtains an expectation value (not necessarily a vacuum expectation value) that is not invariant under the symmetry at issue. This is because the order parameter, which sets a "frame of reference" to be tested against, interacts with other subsystems.
In that situation, the vacuum state does not follow the initial symmetry (which would keep it invariant in the linearly realized Wigner mode, where it would be a singlet), but rather follows the (hidden) symmetry, which is now implemented in the (nonlinear) Nambu–Goldstone mode. Normally, massless Goldstone bosons emerge in the absence of the Higgs process.
The symmetry group might be discrete, like a crystal's space group, or continuous, like space rotational symmetry. Only discrete symmetries can be broken in a vacuum state of quantum theory if the system only has one spatial dimension. A classical solution can break a continuous symmetry, but only if the system has more than one spatial dimension.
Spontaneous Symmetry Breaking In The Higgs Mechanism
Gauge symmetries are responsible for the strong, weak, and electromagnetic forces, among others. In the standard model of particle physics, the Higgs mechanism, or spontaneous symmetry breaking of gauge symmetries, is a key component in explaining metal superconductivity and the creation of particle masses.
One big thing about the difference between true and gauge symmetries is that when a gauge symmetry is broken by accident, it tends to produce big modes, like the plasma mode in a superconductor or the Higgs mode in particle physics, which are both big.
The spontaneous symmetry breaking of the SU(2) U(1) gauge symmetry associated with the electro-weak force provides masses for numerous particles and separates the electromagnetic and weak forces in the standard model of particle physics. The weak interaction is mediated by the W and Z bosons, while the electromagnetic interaction is mediated by the photon.
All of these particles behave similarly at energies far higher than 100 GeV. The Weinberg–Salam theory predicts that this symmetry will be violated at lower energies, allowing the photon and large W and Z bosons to emerge. Furthermore, fermions generate mass in a predictable manner.
The Standard Model of elementary particle interactions demands the presence of a number of particles without spontaneous symmetry breakdown. However, certain particles (the W and Z bosons, for example) would be projected to be massless, despite the fact that they have mass. To circumvent this, the Higgs mechanism is used in conjunction with spontaneous symmetry breaking to give these particles mass.
In addition, it shows that there is a new particle called the Higgs boson, which was found in 2012. Suddenly, a condensate of Cooper pairs breaks the U(1) gauge symmetry that is important for light and electromagnetism. This is like superconductivity in metals.
Spontaneous Symmetry Breaking Example
What Is The Example Of Symmetry Breaking?Many phases in condensed matter physics are examples of spontaneous symmetry breakdown. An order parameter describes each of these systems, describing how the symmetry is disrupted.
- A ferromagnet is a classic example, in which the symmetry of electron spins is disrupted below a specific temperature. The order parameter in this situation is the orientation of spins (local magnetization).
- The crystal structure of most solids is built up of periodic arrays of atoms that aren't invariant across all translations. Spontaneous symmetry breakdown occurs during the creation of solids.
- Another example is liquid-crystal screens. The orientation of the liquid crystals in the display is the order parameter in this case. Applying a voltage changes the order of crystals in a pixel so that it can be turned on or off.
- Although both superconductivity and superfluidity involve spontaneous symmetry violations, the reasons for this are mathematically complex.
What Is Symmetry Breaking And How Did It Occur In The Early Universe?
Pressures and temperatures in the early Universe precluded the permanent development of elementary particles. Until the universe had cooled through the supergravity phase, even quarks and leptons were unable to form stable things.
Conclusion
Symmetry breaking is a crucial step in biological development as well as the evolution of the cosmos as it progresses through different epochs. Symmetry, or at least the initial symmetry, is lost as a structure grows more complicated.
Theorists are seeking to comprehend this symmetry breakdown in reverse, because the cosmos was completely symmetrical at the beginning, and as it cooled, symmetry broke, resulting in the more complex and diverse world of particle physics.

Paula M. Graham
Author

Rhyley Carney
Reviewer
Latest Articles
Popular Articles